Деревья отрезков
Рекомендуемые источники
ИТМО вики-конспекты: Дерево отрезков. Построение
ИТМО вики-конспекты: Реализация запроса в дереве отрезков сверху
ИТМО вики-конспекты: Реализация запроса в дереве отрезков снизу
Habr: Задача RMQ – 2. Дерево отрезков
Вводная
Что если нас часто просят посчитать сумму чисел на некотором подрегионе массива \([from; to)\)? Можно сделать наивную реализацию:
int sum(int from, int to, int[] values) { // from - включительно, to - исключительно
int result = 0;
for (int i = from; i < to; ++i) {
result += values[i];
}
return result;
}
Но асимптотика такого решения будет \(O(to-from)=O(n)\) в худшем случае, где \(n\) - размер массива.
Заметим что \(sum(from, to) = sum(0, to) - sum(0, from)\). Т.к \(sum(0, to) = sum(0, from) + sum(from, to)\), и поэтому \(sum(0, to) - sum(0, from) = sum(0, from) + sum(from, to) - sum(0, from) = sum(from, to)\).
Поэтому достаточно предподсчитать все суммы на префиксе \(sum(0, k)\) и сохранить в специальный массив prefix_sum[k] = sum(0, k).
Теперь достаточно на запрос ответить разницей двух элементов этого массива: sum(from, to) = prefix_sum[to] - prefix_sum[from - 1].
Но что делать если на подотрезке массива хочется например найти максимальное или минимальное значение? Ведь вычесть из максимума на префиксе максимум на другом префиксе уже не выйдет.
Деревья отрезков
Давайте опять что-нибудь предподсчитаем чтобы на базе этих преподготовленных данных быстро (т.е. быстрее чем за линию, т.е. быстрее чем за \(O(n)\)) отвечать на запрос на подотрезке.
Например пусть на подотрезке запрашивается поиск минимума.
Построим дерево следующим образом - на нижнем уровне будет изначальный массив дополненный до ближайшей степени двойки нейтральными-значениями, например в случае поиска минимума это \(+\infty\) (а в случае поиска суммы это был бы \(0\)):
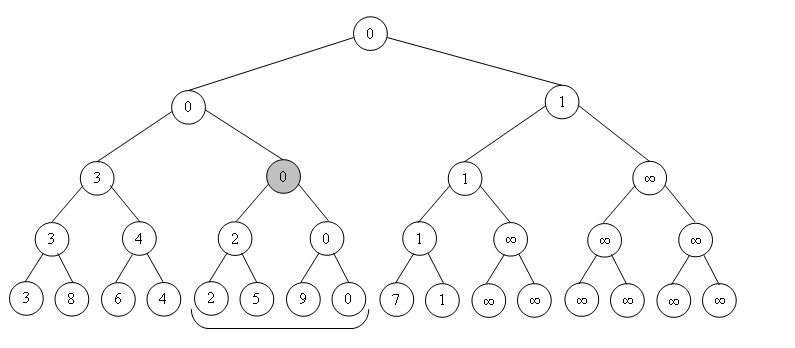
В каждом родительском узле будем хранить результат на всем соответсвующем подотрезке, т.е. по сути - результат применения целевой операции к результату хранящемуся в двух детских узлах.
Но как хранить и как построить данное дерево? А так же как отвечать на каждый запрос?
Представление дерева
Создадим один массив под все дерево, корень дерева будем хранить под индексом \(0\), его детей под индексом \(1\) и \(2\), следующий уровень - \(3-6\), затем \(7-14\) и т.д..
Заметим что тогда:
- У узла под индексом \(i\) два ребенка находятся в массиве под индексами \(2*i+1\) и \(2*i+2\).
- У узла под индексом \(i\) родитель находится в массиве под индексом \((i-1)/2\) (округление вниз).
- Если входной массив размера \(m\) и если округлив его до степени двойки мы получаем \(n\), то первый уровень дерева обладает размером \(1\), второй \(2\) и т.д. вплоть до последнего уровня - самого массива дополненного до степени двойки, т.е. обладающего размером \(n\). Итого массив под дерево нужно аллоцировать размера \(1+2+4+8+...+n=2*n-1\).
Как построить дерево
Достаточно дополнить массив нейтральным элементом до размера-степени двойки. Пусть получился размер \(n\).
Тогда как объяснено выше массив под дерево будет обладать размером \(2*n-1\). При этом изначальный дополненный массив будет располагаться в последних \(n\) ячейках - выкладываем его туда.
Затем нужно посчитать результат операции для каждого узла, это можно сделать от листьев к верхушке, ведь \(tree[i] = min(tree[2*i+1], tree[2*i+2])\).
Как ответить на запрос обходя дерево сверху вниз
Пусть мы хотим реализовать рекурсивную функцию которой на вход дано уже построенное дерево, индекс обрабатываемого в данный момент узла и отрезок интереса \([from; to)\) (первая граница включительна, вторая - исключительна):
int calcNodeL(int node) {
// функция возвращающая левую границу отрезка в изначальном массиве под данным узлом (включительно)
}
int calcNodeR(int node) {
// функция возвращающая правую границу отрезка в изначальном массиве под данным узлом (исключительно)
}
int rangeMin(int[] tree_min, int node, int from, int to) {
int l = calcNodeL(node);
int r = calcNodeR(node);
if (/* отрезок [l; r) не пересекается с [from; to)*/) {
return +inf; // нейтральный элемент, в случае min - это большое число, в случае sum - это ноль
} else if (/* отрезок [l; r) содержится в [from; to)*/) {
return tree_min[nodes];
} else {
int childL = 2 * node + 1;
int childR = 2 * node + 2;
// Спускаемся в обоих детей, ищем минимум в каждом из них, и из этих двух минимумов возвращаем самый маленький
return min(rangeMin(tree_min, childL, from, to), rangeMin(tree_min, childR, from, to));
}
}
Определять диапазон в массиве который покрывает узел можно одним из следующих способов:
1) Хранить в каждом узле не только значение результата на подотрезке (наприм сумма или минимум), но и собственно int l, int r. Для этого нужно либо завести еще два массива int[] tree_l и int[] tree_r, либо в каждом узле дерева хранить объект своего класса class TreeNode { int result; int l; int r; }
2) Явным образом передавать int l, int r как аргументы функции наравне с int node, int from, int to. И при рекурсивном вызове rangeMin у детей передавать туда соответствующий диапазон, например \([l; (l+r)/2)\) для левого ребенка, и \([(l+r)/2; r)\) - для правого.
Как ответить на запрос обходя дерево снизу вверх
Пусть мы не хотим связываться с calcNodeL, calcNodeR и рекурсией.
В таком случае давайте заметим что если изначальный запрос \([from; to)\), то эти элементы в дереве лежат по индексам \([n-1+from; n-1+to)\), давайте заменим наш отрезок запроса на этот новый, т.е. сделаем замену \(from=n-1+from\) и \(to=n-1+to\).
Тогда если \(from \% 2 == 1\) и \(to \% 2 == 1\), то задачу можно свести к запросу на предыдущем уровне для индексов \([(from-1)/2; (to-1)/2)\).
Но что делать если так сделать нельзя? Достаточно взять те одиночные элементы по краям которые нам не позволяют это сделать, добавить к текущему результату, и вновь сделать возможным переход в родителя.
Зачем же рекурсивный обход сверху вниз, раз он сложнее?
В рамках рекурсивного обхода несложно поддержать еще один запрос: проделать одну и ту же операцию над всеми элементами на отрезке. Например это может быть операция добавить к каждому элементу данное число или заменить каждый элемент на данное число.
Основная идея - давайте лениво в каждом узле хранить информацию о проведенной операции если ее провели над всеми элементами подотрезка данного узла. Соответственно когда приходит запрос на изменение - этот запрос размазывается лишь по небольшому числу узлов за логарифмическую асимптотику.
Подробнее можно прочитать здесь.
Доп. задачки
1) Найти число различных чисел на подотрезке.
2) Найти число убывающих подпоследовательностей длины три. Изменится ли задача если бы требовалось находить число подпоследовательностей как обычно на многих подотрезках, а не просто среди всего массива?